特征湍流

发表评论

© Written by J.Y. WANG

自然风状态下的大气边界层湍流可以看作是由平均风输运的一些尺度不同的旋涡的叠加；在统计上，可被处理为一平稳的高斯过程，采用达文波特谱或其他脉动风速谱来描述。当大气边界层湍流遇到建筑物后，会不可避免的产生分离、再附、旋涡脱落等现象，使其内部结构遭到破坏，此时的流动过程在统计特性上已明显区别于自然风状态下的大气边界层湍流，且与结构本身的几何特性密切相关，因此称之为特征湍流。

 

图2.2 大跨度屋盖结构绕流示意图

特征湍流的形成主要与流体的粘性效应有关，当风绕建筑物流动时，与结构表面接触的流体微粒会贴附在结构表面上；由于粘性效应靠近表面的一层流体微粒将减慢流动，形成跗面层；这一过程一直持续到粘性力减弱为零，此时的流体微粒流动速度就等于外层气流的速度。当附面层的外层流速大于内层流速时，就会在附面层内形成较大的逆压梯度，导致附面层分离。分离作用形成了一系列离散旋涡，并脱落到钝体后方的尾流中，这些旋涡使得分离点附近出现非常大的吸力。在一定的来流湍流强度和攻角条件下，自建筑物前缘分离的附面层会再附到建筑物表面，这时附面层下会形成不通气的空腔（分离泡），使得靠近建筑物前缘的附面层下产生负压。

特征湍流对屋盖风荷载的作用可以概括为以下几方面：

（1）屋面风压主要以风吸力为主，并直接导致屋面出现局部风吸力极值。

（2）使屋面的大部分区域处于来流的再附区，由于再附作用是在分离泡破碎后形成的，此时旋涡的组织结构已经被破坏，因此屋盖表面的风压相关性总体较弱。

（3）拟定常假设无法无法适用。目前风荷载作用的估计通常都基于拟定常假设，即建筑物表面的风压与大气边界层来流之间具有完全的相关性，即屋面风压的变化特性与来流的变化特性一致，二者之间的关系可以用Bernoulli方程表示。Kawai（1983）曾对方柱表面的脉动风压功率谱进行过测量，结果如下图所示。可以看出，在迎风面脉动风压的功率谱与大气来流的Karman谱十分接近，说明在迎风面上可以采用拟定常假定；但是在来流平行的侧表面上，脉动风压的功率谱则与根据拟定常假设所确定的功率谱差别较大，而这种差别正是由于来流的分离和再附作用造成的。

 

图2.3 方柱表面脉动风压功率谱

研究表明，特征湍流是导致建筑物表面出现局部风压极值的主要原因，研究特征湍流的发生、发展过程，对于认识建筑物的风致破坏机理具有十分重要的意义。在这方面，国外的学者已开展了一些研究。Kawai借助热线探头测量低矮屋盖上方的绕流场，得到旋涡中心的平均位置，即旋涡速度场旋转中心的位置，结果证实位于屋盖表面最大风吸位置之上；Bienkiewicz将低矮房屋屋盖拐角区域的风压分布同流场可视化结果进行了比较，认为风压变化梯度最大的位置为屋盖上旋涡的再附处；Kawai和Nishimura同步测的低矮平屋盖表面风压及来流风速时程，基于整个屋盖表面风压脉动相关性得出屋盖上方作用的一对锥形涡在横风向出现同步交替波动，如下图所示，即锥形涡形状不变，但轴线OB、OD同步波动到OA、OC，使得关于屋盖对角线对称点的风压呈反相变化。但是以上的研究对象主要是低矮建筑，对于大跨度屋盖的研究还很少。由于大跨度屋盖表面风压特性不仅与来流特性有关，还会的更多的受到建筑物自身特征湍流的影响。因此研究大跨度屋盖的特征湍流特性，对于完善大跨度屋盖抗风设计具有重要意义。

 

图2.4 低矮房屋平屋盖上锥形涡的交替波动

由于特征湍流的复杂性，目前还没有形成一套成熟的分类方法，以下只给出几种常见的特征湍流形式。如当来流垂直于平屋盖迎风外边缘时，来流在平屋盖的前缘会发生分离，形成一个明显的柱状涡；当来流同平屋盖外边缘有夹角时，会形成一对锥状涡；及高层建筑在侧面形成的马蹄涡，也称移动式锥形涡等，这些都是特征湍流典型的旋涡形式。

 

图2.5 柱状涡和锥形涡

 

图2.6 马蹄涡

CFX数值风洞模拟范例

发表评论

© Written by J.Y. WANG

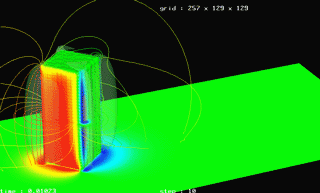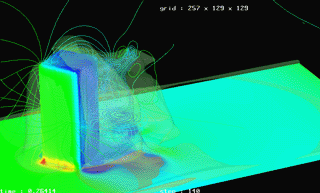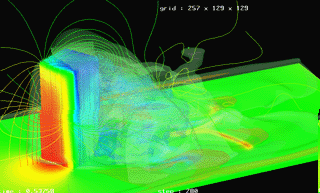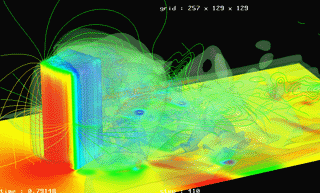
数值风洞模拟范例——

仅CFX前处理及求解定义部分

 

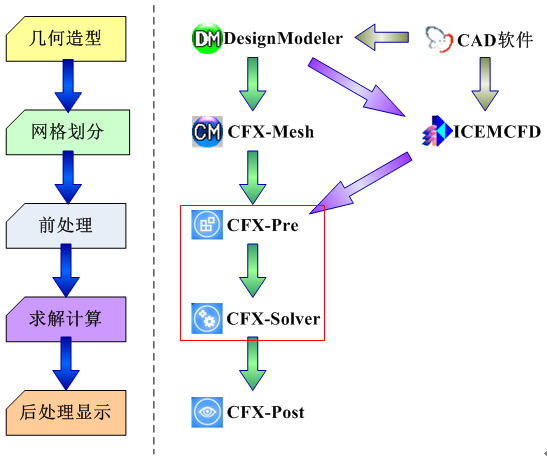
CFD数值模拟过程

 

CFX前处理及求解定义：

1.导入网格（Import Mesh）

2.定义模拟类型（Simulation Type）

3.创建计算域（Domain）

4.指定边界条件（Boundary Condition）

5.给出初始条件（Initial Conditions）

6.定义求解控制（Solver Control）

7.定义输出数据（Output File & Monitor Points）

8.写入定义文件（.def File）并求解

Starting CFX-Pre

1.  Prepare the working directory using the following files in the examples directory:

  • WindProfile.ccl
  • BluntBodyMesh.gtm

2.  Set the working directory and start CFX-Pre.

Defining a Case in CFX-Pre

1.  In CFX-Pre, select File > New Case.

2.  Select General and click OK.

3.  Select File > Save Case As.

4.  Under File name, type BluntBody.

5.  Click Save.

Importing the Mesh

  1. Edit Case Options > General in the Outline tree view and ensure that Automatic Default Domain is turned off.

Default Domain generation should be turned off because you will create a new domain manually, later in this tutorial.

  1. Right-click Mesh and select Import Mesh > Other. The Import Mesh dialog box appears.
  2. Apply the following settings:
Setting Value
File name BluntBodyMesh.gtm
  1. Click Open.

Importing CEL Expressions

1.  Select File > Import > CCL.

2.  Ensure that Import Method is set to Append.

3.  Select WindProfile.ccl, which should be in your working directory.

4.  Click Open.

LIBRARY:

CEL:

EXPRESSIONS:

zb = 10 [m]

ub = 29.2 [m s^-1]

Ht = 350 [m]

Lu = 30 [m]

alpha = 0.16 []

uz = if( z>zb, ub*((z+0.00001[m])/zb)^alpha, ub )

Iz = if( z>zb, 0.1*(Ht/(z+0.00001[m]))^(alpha+0.05), 0.31 )

kz = 1.5*(Iz*uz)^2

ez = 0.09^0.75*(kz^1.5)/Lu

END

END

END

Setting the Analysis Type

  1. Click Analysis Type.
  2. Apply the following settings:
Tab Setting Value
Basic Settings Analysis Type > Option Steady State
  1. Click OK.

Creating the Domain

  1. Ensure that Flow Analysis 1 > Default Domain is deleted. If not, right-click Default Domain and select Delete.
  2. Click Domain, and set the name to BluntBody.
  3. Apply the following settings to BluntBody:
Tab Setting Value
Basic Settings Location and Type > Location Fluid
Fluid and Particle Definitions Fluid 1
Fluid and Particle Definitions > Fluid 1 > Material Air Ideal Gas
Domain Models > Pressure > Reference Pressure 1 [atm]
Fluid Models Heat Transfer > Option Isothermal
Heat Transfer > Fluid Temperature 20 [C]
Turbulence > Option Shear Stress Transport

Creating the Boundaries

Inlet Boundary

1.  Click Boundary.

2.  Under Name, type Inlet.

3.  Apply the following settings:

Tab Setting Value
Basic Settings Boundary Type Inlet
Location Inlet
Boundary Details Flow Regime > Option Subsonic
Mass and Momentum > Option Cart. Vel. Components
Mass and Momentum > U uz
Mass and Momentum > V 0 [m s^-1]
Mass and Momentum > W 0 [m s^-1]
Turbulence > Option k and Epsilon
Turbulence > Turb. Kinetic Energy kz
Turbulence > Turb. Eddy Dissipation ez

4.  Click OK.

Outlet Boundary

1.  Create a new boundary named Outlet.

2.  Apply the following settings:

Tab Setting Value
Basic Settings Boundary Type Outlet
Location Outlet
Boundary Details Mass and Momentum > Option Opening Pres. And Dirn
Mass and Momentum > Relative Pressure 0 [Pa]
Flow Direction > Option Normal to Boundary Condition
Turbulence > Option Zero Gradient

3.  Click OK.

Free-Slip Wall Boundary

1.  Create a new boundary named FreeWalls.

2.  Apply the following settings:

Tab Setting Value
Basic Settings Boundary Type Wall
Location FreeWalls
Boundary Details Mass and Momentum > Option Free Slip Wall

3.  Click OK.

Wall Boundary on the Blunt Body Surface

1.  Create a new boundary named Body.

2.  Apply the following settings:

Tab Setting Value
Basic Settings Boundary Type Wall
Location Body
Boundary Details Mass and Momentum > Option No Slip Wall

3.  Click OK.

Setting Initial Values

The initial conditions are consistent with inlet boundaries.

  1. Click Global Initialization .
  2. Apply the following settings:
Tab Setting Value
  Initial Conditions > Cartesian Velocity Components > Option Automatic with Value
  Initial Conditions > Cartesian Velocity Components > U uz
  Initial Conditions > Cartesian Velocity Components > V 0 [m s^-1]
  Initial Conditions > Cartesian Velocity Components > W 0 [m s^-1]
  Initial Conditions > Static Pressure > Option Automatic with Value
  Initial Conditions > Static Pressure > Relative Pressure 0 [Pa]
  Initial Conditions > Turbulence > Option k and Epsilon
Global Settings Initial Conditions > Turbulence > Turbulence Kinetic Energy > Option Automatic with Value
Initial Conditions > Turbulence > Turbulence Kinetic Energy > Value kz
Initial Conditions > Turbulence > Turbulence Eddy Dissipation > Option Automatic with Value
Initial Conditions > Turbulence > Turbulence Eddy Dissipation > Value ez
  1. Click OK.

Setting Solver Control

  1. Click Solver Control .
  2. Apply the following settings:
Tab Setting Value
  Advection Scheme > Option Specified Blend Factor
  Advection Scheme > Blend Factor 0.75
  Turbulence Numerics > Option High Resolution
Basic Settings Convergence Control > Max. Iterations 100
Convergence Control > Fluid Timescale Control > Timescale Control Physical Timescale
Convergence Control > Fluid Timescale Control > Physical Timescale 2 [s]
Convergence Criteria > Residual Target 1e-05
  1. Click OK.

Obtaining a Solution in Serial

1.  Click Start Run.

2.  When CFX-Solver is finished, select the check box next to Post-Process Results.

3.  If using Standalone Mode, select the check box next to Shut down CFX-Solver Manager.

4.  Click OK.

Obtaining a Solution with Local Parallel

To run in local parallel mode, the machine you are on must have more than one processor.

In CFX-Solver Manager, the Define Run dialog box should already be open.

1.  Leave Type of Run set to Full.

If Type of Run was instead set to Partitioner Only, your mesh would be split into a number of partitions but would not be run in the CFX-Solver afterwards.

2.  Set Run Mode to a parallel mode suitable for your configuration; for example, HP MPI Local Parallel.

This is the recommended method for most applications.

3.  If required, click Add Partition to add more partitions.

By default, 2 partitions are assigned.

4.  Select Show Advanced Controls.

5.  Click the Partitioner tab at the top of the dialog box.

6.  Use the default MeTiS partitioner.

Your model will be divided into two sections, with each section running in its own CFX-Solver process. The default is the MeTiS partitioner because it produces more efficient partitions than either Recursive Coordinate Bisection or User Specified Direction.

7.  Click Start Run.

8.  When CFX-Solver is finished, select the check box next to Post-Process Results.

9.  If using Standalone Mode, select the check box next to Shut down CFX-Solver Manager.

10. Click OK.

 

空间结构形态学的研究现状

发表评论

© Written by J.Y. WANG

目前国内的空间结构形态学研究处于起步阶段，而国外的形态学研究也才从20世纪末才有所发展，还没有形成一个系统的理论框架作为形态学的研究基础，仅仅是从内容上对空间结构形态学的一些方面作了相关的研究，并且在工程实践方面的经验也较少。本文从结构外形和结构内部拓扑关系的构思两方面按所使用的方法对当前空间结构形态学的研究发展和现状做一个大致的归类和总结。

许多建筑学家和结构学家为了寻求合理的结构形态，探索和尝试了很多方法。目前结构形态的构思主要有：几何生成法、物理生成法、数值生成方法和仿生学方法等。

几何生成方法

几何生成法是构造曲面的最基本方法（如图1-6所示）。根据几何学的基本原理，可大致采用以下几种途径：1）对曲线进行平移、缩放、旋转等操作，进而生成一系列相对规则的曲面；2）直纹曲面，使相同长度的直线段通过已知导线从而生成曲面；3）解析曲面，即有数学解析表达式的曲面；4）非均匀有理B样条曲面，即以B样条函数插值的方式得到曲面，与前面几种方法相比，该方法可以生成任意曲面形式，因而在自由曲面形态研究中具有更加广泛的适用性。与曲面的创建同等重要的是对于曲面的切割、组合等基本操作,它可以展示出各种各样的变化形态。其中图1-7为某火车站的成形过程，该曲面采用了大小两个圆环进行切割得到，著名的奥运场馆“鸟巢”的成形也是采用了类似的曲面生成技术。图1-8演示了如何通过几个相连球的切面来构造自由曲面。

 

图1-6 曲面的几何生成方法

现在的几何曲面创构趋势是脱离简单的几何曲面形式向更自由的形态发展。如组合圆弧旋转曲面的切割（大馆树海穹顶），平移曲面（柏林动物园河马馆，1997年）等。在理论方面，2004年美国的Edgar Stach介绍了自1838年Henry Moseley开始研究贝类形态以来继随后的Thompson, Raup, Cortie, Dawkins等研究其本人的最新研究成果。2004年德国的James Glymph, Dennis Shelden, Cristiano, Judith Mussel, Hans Schober等系统的总结了表面平移法。

  a) 几何原型                           b) 建筑鸟瞰图                         c) 建筑内景

图1-7 曲面切割实例

 

图1-8 曲面的组合实例

物理生成方法

物理生成方法是借助力学原理来生成曲面即由平衡形状与力流、或者由形态抵抗而联想到的形与力的结合形态。相对于几何生成法，这种方法更注重了曲面的力学合理性。根据现有文献可总结为以下几类（如图1-9所示）：

 

自由曲面建模的物理方法

1．悬挂索网法：通过在无初始预张力的索网上面施加自重荷载后固定成型得到。

2．气泡膜法：通过薄膜的势能在表面张力作用下会达到最小值而形成极小曲面的方法；

3．充气膜法：通过对膜施加内压而生成曲面；

4．预应力索网法：对索网结构施加预应力，并通过找形的方法形成初始几何形状。

5．其他力学方法。

数值生成方法

随着计算机技术不断地发展，在分析方法的基础上进行结构形态的数值生成成为可能。其中应用到工程实际的改进进化论方法和高度调整法取得了很好的效果。改进进化论方法就是模仿自然界进化现象，根据Mises应力等值线（面）对结构进行“保留、淘汰、补充”等操作，使之逐步演变成应力均匀的结构。图1-10所示为该方法的工程实例。高度调整法是根据应变能对曲面形状变化的敏感程度，不断调整曲面上各点的高度，最终得到一个应变能最小的合理曲面形态。图1-11为该方法的工程实例。

 
图1-10 卡塔尔教育城会展中心（注：250.0 m长×30.0 m宽×20.0 m高，两支承点间的距离为100m。）
 
图1-11 日本福冈市中央公园中心设施

仿生生成方法

自然总是趋向于用最有效的方式来组织其内部结构。因此，自然界的各种构形就成为理想的建筑构思源泉。例如，如图1-12所示我们惊奇发现自然界中的冰川和贝壳面居然在不同的环境下采用相同的形态保持它们自身的稳定。仿生学的形态以自然界某些生物体功能组织和形象构成规律为研究对象，通过探寻自然界中科学合理的建造规律而模拟的形态。它的主要研究方法就是提出模型，进行模拟。其研究程序大致有以下三个阶段：

首先是对生物原型的研究。根据生产实际提出的具体课题，将研究所得的生物资料予以简化，吸收对技术要求有益的内容，取消与生产技术要求无关的因素，得到一个生物模型；第二阶段是将生物模型提供的资料进行数学分析，并使其内在的联系抽象化，用数学的语言把生物模型“翻译”成具有一定意义的数学模型；最后数学模型制造出可在工程技术上进行实验的实物模型。

  a) 冰川                                          b) 贝壳
 图1-12 自然界中的贝壳形

但无论是哪类形态构思，若想在钢筋混凝土及薄膜材料之外创造出此种曲面，其构成方法是一个重要的课题。也就是说不管是预制法，还是金属线材，都要求在单元的集成与网格的分割仔细研究即空间网格结构的拓扑结构。最近的网格设计趋势是脱离简单的网格形式向更自由的、更多样发展（如图13所示）。例如最近工程国家游泳中心（水立方）的网格是由气泡阵列理论经12面体和14面体填充空间后用平面切割构成的网格形式；国家体育场（鸟巢）的在主框架确定后随机附以编织物线条构成的网格形式。在理论方面，1997年美国的J. Fonseca提出了由力线确定传力路径的思想。2004年美国的Edgar Stach从生物界的形态优化角度阐述了基于气泡理论的自然界的自增生结构。2004年丹麦的T. Wester从自然界图像观察中提出的基于机动分析的几何构成网格设计概念，阐述了点、线、面空间关系及其对偶准则，解释了七十年代中期Roger Penrose发现的二维Penrose图及八十年代中期Dan Schechtman发现的三维的Penrose图。2006年以色列的Michael BURT进一步阐述了其1966年提出的由周期多孔曲面和周期多孔多面体生成网格的概念，以及十九和二十世纪相关数学界对此问题的进展[19]。

 

图1-13 新颖的空间网格结构拓扑构造方法

空间结构形态学的研究内容

发表评论

© Written by J.Y. WANG

​写在前面的话

什么是美的？

人类经过千百年的进化，对于美的认识，是通过对自然界的观察和感悟形成的。而自然界的这些物体的形状与结构是符合物理规则的，简单的说是受力合理的。那么经过世代遗传必然在大多数正常人类心中所认为的美，也应是在力学上合理。

这就可以产生一个推论，虽然结构合理的建筑不一定是美的，但一个优美的建筑必然应是结构合理的。结构合理是建筑优美的必要条件。

而当今的建筑师，有些严重偏离了这一基本美学规律，奇奇怪怪、哗众取宠者屡见不鲜。建议在建筑师培养中加强结构和力学相关方面的教育。

英国动物学家汤普森有一句名言“形是力的图解”，这句话恰恰体现了形态学的本质，即形态学认为自然界中的物体的形与其内部的结构之间构成了有机的整体；因此，结构的外部形式、内部构造和功能三者之间应该是和谐统一的。形态学就是研究各种形状与其内部结构之间关系的科学。按照结构形态学的观点，一个优秀的建筑不仅应该能够表现出建筑物本身的艺术价值，更应该具有良好的受力性能。但是在现实情况下要实现这一目标还是相当困难的，这主要源于现阶段设计步骤的不合理性，即建筑设计在先，结构设计在后。由于专业知识的局限性，由建筑设计所产生的曲面在力学性能上很可能是不合理的，而后结构工程师只能在这一不尽合理的几何形状基础上设计结构的受力构件，从而产生了最终建筑产品的不合理性。而实际上一个优秀的建筑作品应该是建筑师与结构工程师相互协作、相互促进来完成的，而不是平行进行，没有交集的机械创作。

                                          图1-5 结构形态学的研究内容
 

合理的结构形态应同时满足以下两方面要求：1）丰富的建筑艺术表现形式；2）结构受力合理。一般来说，一个结构的优劣主要取决于它的内力分布模式是否合理，为评价结构的合理性，需要引入了结构形态的概念。如前所述，“结构形态”应包括两方面基本内容：第一是结构的 “形”，其次是结构的“态”。结构的“形”是指包括结构的几何外形、杆件的布置方式、以及构件尺寸等结构的外在特征；结构的“态”是指结构在外荷载作用下的内力分布状态，是结构的内在反应。具有特定几何外形的结构在荷载作用下，其内力分布状态是一定的；而已知一个特定的内力分布状态却不能确定唯一的建筑几何外形。因此，对结构形态的研究是评价结构好与坏的基本参数，一个合理的建筑几何外形才能对应有一个较优的受力状态。

对于结构形态的研究一般可分为以下三个层面：1）几何外形的创建与优化，这一层面主要研究结构的整体几何外形；2）杆件布置关系的创建与优化，这一部分主要研究以何种方式布置杆件更为合理的问题；3）杆件截面的确定与优化。从现有研究来看，第三层面的研究已经大范围的开展，而第一、二层面的内容将是未来研究的重点。

空间结构形态学的发展

2条回复

© Written by J.Y. WANG

结构形态学是从整体上研究建筑形状与结构受力之间的关系，目的在于寻求二者的协调统一。空间结构形式十分丰富多彩，而且往往凭借其合理形体来实现结构的高效率，因此形态学研究对空间结构具有重要意义。空间结构形态学的发展大致分为三个阶段：

1、早期的探索与实践

      a) 拱桥                       b) 穹顶                         c) 悬索桥                   d) 帐篷

图1-1 早期探索和实践的合理结构形态

人类通过长期的生产实践，发现和创造了许多合理的结构（建筑）形式。如拱桥、穹顶、悬索桥、帐篷等。

2、有意识的结构形态学研究活动

在空间结构发展早期，计算机尚未普及的时候，物理方法的应用较多，这一时期结构形态学进入了一个有意识的研究阶段。其中颇具代表性的方法是由西班牙建筑师A.Gaudi在20世纪初提出的“逆吊实验方法”，并利用其设计了一些砖石结构的教堂建筑（巴塞罗那的萨哥拉达·伐米利亚大教堂，如图1-2a所示）.

   
a) 伐米丽亚大教堂 b) 戴丁根加油站
图1-2 逆吊实验法及其实践

瑞士工程师H.Isler于上世纪60、70年代，继承发展了“逆吊实验方法”设计了许多混凝土薄壳结构。图1-2b所示的戴丁根加油站即为逆吊实验法的一个工程实例。其成形过程为，对一个无初始张力的索网结构上加入石膏等易凝结的材料，在材料自重作用下结构只受到拉力的作用，待材料凝固后将整个结构翻转，此时结构在自重荷载作用下即为一个纯粹的受压结构。

虽然利用“逆吊实验方法”所得到的曲面结构形态只存在面内压应力均匀分布的凸型形状，但它突破了从传统的几何形状范围内选择的做法，实现了根据设计条件求出合理曲面结构形态的设计。

   
a) 短程线穹顶和张拉整体结构 b) 肥皂膜试验确定索膜结构
 
c) 表面平移法工程实例
图1-3 结构形态研究取得的一些成果

同样在这一阶段结构形态学在其它方面也进行了探索并取得了一定得成果。上世纪50至70年代美国发明家B.Fuller通过对一些自然现象的观察和思考，提出了短程线穹顶和张拉整体的思想，如图1-3a所示。而60、70年代时德国建筑师F.Otto 利用肥皂膜试验，解决了索膜结构的初始形态确定问题，如图1-3b所示。进入80、90年代时德国工程师J.Schlaich利用几何平移和缩放的方法，设计了许多自由曲面轻型结构，如图1-3c所示。

3、将分析方法引入结构形态学研究

上世纪80年代，日本半谷教授采用 “广义逆矩阵”理论解决了悬索结构等形状不稳定结构的初始形态确定问题（如图1-4）。90年代半谷教授在以往研究的基础上系统提出了结构形态创构概念——针对具体工程，利用分析方法，采用不同的约束条件，寻求建筑物的多种 “良好形状”。

 
图1-4 悬垂型形状确定的广义逆矩阵法

最近在国际上结构形态创构方法的理论研究开展得比较活跃，逐步得到了世界各国建筑届的重视。目前提出的理论方法有“均匀化方法”、“Bubllf法”、“成长变形法”、“适应成长法”、“渐进法（ESO）”、“遗传算法（GA）”、“悬垂型壳体形状决定法”、“以应力分布为目标函数的曲面形状创构法”等，这些方法解决了不少特定类型问题。虽然理论上远未定型，得到的结构形状非常单调，尚不能应用到工程实际，但它开辟了利用理论方法求结构形态的可能性。